1. পূর্বপাঠের পুনরালোচনা | কষে দেখি 1.4 | Exercise 1.4 | Ganit Prabha Class VII math solution | WBBSE Class 7 Math Solution in Bengali
কষে দেখি 1.4 সমাধান
1. নীচের চিত্রগুলির পরিসীমা মাপিঃ
.png)
ত্রিভুজটির পরিসীমা
= (8+\ 5+8) সেমি.
= 21 সেমি.
.png)
ত্রিভুজটির পরিসীমা
= (5 + 10 + 12) সেমি.
= 27 সেমি.
.png)
চিত্রটির পরিসীমা
= (8+8+8+8) সেমি.
=32 সেমি.
.png)
উপরের চিত্রটির পরিসীমা
= (10+4+4+10+4+4) সেমি.
= 46 সেমি.
.png)
উপরের চিত্রটির পরিসীমা
= (10+20+10+20) সেমি.
= 60 সেমি.
.png)
উপরের চিত্রটির পরিসীমা
= (6+8+3+3+8) সেমি.
=28 সেমি.
2. নীচের চিত্রগুলি কতটা জায়গা দখল করে আছে দেখি।
[প্রতিটি ক্ষুদ্রতম বর্গঘর 1 বর্গসেমি.]
%20image.png)
(a) চিত্রটি 50 টি ঘর দখল করে আছে।
∴ (a) চিত্রটি 50 বর্গসেমি. জায়গা দখল করে আছে।
(b) চিত্রটি 48 টি ঘর দখল করে আছে।
∴ (b) চিত্রটি 48 বর্গসেমি. জায়গা দখল করে আছে।
(c) চিত্রটি 48 টি ঘর দখল করে আছে।
∴ (c) চিত্রটি 48 বর্গসেমি. জায়গা দখল করে আছে।
(d) চিত্রটি 42 টি ঘর দখল করে আছে।
∴ (d) চিত্রটি 42 বর্গসেমি. জায়গা দখল করে আছে।
(e) চিত্রটি 51 টি ঘর দখল করে আছে।
∴ (e) চিত্রটি 51 বর্গসেমি. জায়গা দখল করে আছে।
(f) চিত্রটি দখল করেছে \(\left(24+\frac{12}{2}\right)\) টি (প্রায়)
= (24+6) টি (প্রায়)
= 30 টি (প্রায়)
∴ (f) চিত্রটি 30 বর্গসেমি. (প্রায়) জায়গা দখল করে আছে।
3. নিজেরা ছক-কাগজ তৈরি করে 25 বর্গঘর, 40 বর্গঘর, 36 বর্গঘর ও 62 বর্গঘর দখল করে আছে এমন চিত্র আঁকি।
%20image.png)
(a) চিত্রটি 25 বর্গঘর, (b) চিত্রটি 40 বর্গঘর, (c) চিত্রটি 36 বর্গঘর
এবং (d) চিত্রটি 62 বর্গঘর দখল করে আছে।
4. নীচের ছক-কাগজের বর্গক্ষেত্রগুলোর এক একটি বাহুর দৈর্ঘ্য মাপি এবং ক্ষেত্রফল নির্ণয় করি। [ধরি, একটি ক্ষুদ্রতম বর্গঘর = এক বর্গসেমি.]
%20image.png)
a) বর্গক্ষেত্রটির বাহুর দৈর্ঘ্য 5 সেমি.
∴ বর্গক্ষেত্রটির ক্ষেত্রফল
\(=5\times5\) বর্গসেমি.
= 25 বর্গসেমি.
b) বর্গক্ষেত্রটির বাহুর দৈর্ঘ্য 8 সেমি.
∴ বর্গক্ষেত্রটির ক্ষেত্রফল
\(=8\times8\) বর্গসেমি.
= 64 বর্গসেমি.
c) বর্গক্ষেত্রটির বাহুর দৈর্ঘ্য 11 সেমি.
∴ বর্গক্ষেত্রটির ক্ষেত্রফল
\(=11\times11\) বর্গসেমি.
= 121 বর্গসেমি.
d) বর্গক্ষেত্রটির বাহুর দৈর্ঘ্য 9 সেমি.
∴ বর্গক্ষেত্রটির ক্ষেত্রফল
= 9 × 9 বর্গসেমি.
= 81 বর্গসেমি.
5. বর্গমূল নির্ণয় করিঃ
(a) \(5^2\times8^2\)
সমাধানঃ
\(5^2\times8^2\) এর বর্গমূল \(=5\times8=40\)
(b) 4225
সমাধানঃ
\(4225\ =5\times5\times13\times13\)
\(=5^2\times{13}^2\)
∴ \(\sqrt{4225}=5\times13=65\)
(c) 10609
সমাধানঃ
\(10609\ =\ 103\ \times\ 103\)
∴ \(\sqrt{10609}=\sqrt{103\times103}=103\)
(d) 108241
সমাধানঃ
∴ \(\sqrt{108241}=329\)
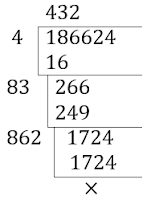
(e) 186624
সমাধানঃ
∴ \(\sqrt{186624}=432\)
(f) \(\left({24}^2+{10}^2\right)\)
সমাধানঃ
\(\left({24}^2+{10}^2\right)\)
= (576+100)
= 676
∴ \(\sqrt{676}=26\)
6. 3000 -এর নিকটতম পূর্ণবর্গ সংখ্যা খুঁজি যা (a) 3000 থেকে বড়ো (b) 3000 এর থেকে ছোটো।
সমাধানঃ
\({50}^2=2500,\ {51}^2=2601,\ {52}^2=2704,\)
\( {53}^2=2809, {54}^2=2916,\ {55}^2=3025\)
3000 এর নিকটতম পূর্ণবর্গ সংখ্যা দুটি হল 2916 এবং 3025
(a) 3000 এর থেকে বড়ো এবং নিকটতম পূর্ণবর্গ সংখ্যা হল 3025
(b) 3000 এর থেকে ছোটো এবং নিকটতম পূর্ণবর্গ সংখ্যা হল 2916
7. 9545 থেকে কোন ক্ষুদ্রতম ধনাত্মক পূর্ণসংখ্যা বিয়োগ করলে বিয়োগফল একটি পূর্ণবর্গ সংখ্যা হবে হিসাব করে দেখি।
সমাধানঃ
∴ 9545 থেকে 136 বিয়োগ করলে বিয়োগফল একটি পূর্ণবর্গ সংখ্যা হবে।
8. 5050 -এর সঙ্গে কোন ক্ষুদ্রতম ধনাত্মক পূর্ণসংখ্যা যোগ করলে যোগফল একটি পূর্ণবর্গ সংখ্যা হবে।
সমাধানঃ
71 এর পরবর্তী পূর্ণসংখ্যার বর্গ \(={72}^2=5184\)
∴ 5050 এর সঙ্গে যে ক্ষুদ্রতম ধনাত্মক পূর্ণসংখ্যা যোগ করলে যোগফল একটি পূর্ণবর্গ সংখ্যা হবে সেই
সংখ্যাটি হল (5184-5050) = 134
9. বারুইপুরের এক পেয়ারা বাগানে 1764 টি পেয়ারাগাছ লাগানো হয়েছে। যতগুলি সারিতে পেয়ারাগাছ লাগানো হয়েছে প্রতি সারিতে ততগুলি পেয়ারাগাছ আছে। হিসাব করে দেখি প্রতি সারিতে কতগুলি পেয়ারাগাছ আছে।
সমাধানঃ
∴ \(\sqrt{1764}=42\)
∴ প্রতি সারিতে 42 টি পেয়ারাগাছ আছে।
10. হোমিওপ্যাথি ওষুধ রাখার বাক্সে 1225 টি শিশির রাখার ঘর আছে। ঘরগুলি এমনভাবে সাজানো আছে যে যতগুলি সারি আছে প্রতি সারিতে ততগুলি ঘর আছে। হিসাব করে দেখি বাক্সে কতগুলি সারি আছে।
সমাধানঃ
∴ \(\sqrt{1225}=35\)
∴ বাক্সে 35 সারি আছে।
11. তিনটি ধনাত্মক পূর্ণসংখ্যার প্রথম ও দ্বিতীয়টির গুণফল 24, দ্বিতীয় ও তৃতীয়ের গুনফল 48 এবং প্রথম ও তৃতীয়ের গুণফল 32; সংখ্যা তিনটি কী কী তা হিসাব করে দেখি।
সমাধানঃ
প্রথম সংখ্যা × দ্বিতীয় সংখ্যা = 24
দ্বিতীয় সংখ্যা × তৃতীয় সংখ্যা = 48
প্রথম সংখ্যা × তৃতীয় সংখ্যা = 32
∴ প্রথম সংখ্যা\(^2\) × দ্বিতীয় সংখ্যা\(^2\) × তৃতীয় সংখ্যা\(^2\)
=24 × 48 × 32
∴ প্রথম সংখ্যা × দ্বিতীয় সংখ্যা × তৃতীয় সংখ্যা
\(=\sqrt{24\times48\times32}\)
\(=\sqrt{4\times6\times6\times8\times8\times4}\)
\(=4\times6\times8=192\)
∴ প্রথম সংখ্যা \(=\frac{192}{48}=4\),
দ্বিতীয় সংখ্যা \(=\frac{192}{32}=6\)
এবং তৃতীয় সংখ্যা \(=\frac{192}{24}=8\)
12. শিবাজি সংঘের ক্লাবে যতজন সদস্য আছে প্রত্যেকে সদস্য সংখ্যার পাঁচগুণ টাকা চাঁদা দিয়েছে। 515205 টাকা চাঁদা উঠেছে। হিসাব করে দেখি ক্লাবের সদষ্য সংখ্যা কত?
সমাধানঃ
যতজন সদস্য আছে প্রত্যেকে তত চাঁদা দিলে চাঁদা
উঠত \(\frac{515205}{5}\) টাকা \(=103041\) টাকা
∴ \(\sqrt{103041}=321\)
∴ ক্লাবের সদস্য সংখ্যা 321 জন।
13. দার্জিলিং এর এক বাগানের মালিক মোট 1080 টি কমলালেবু পেড়েছেন। সেই কমলালেবু কতগুলি ঝুড়ি এনে তাঁর প্রতিটিতে ঝুড়ির সংখ্যার সমান কমলালেবু রাখতে গিয়ে দেখেন 9 টি কমলালেবু কম পড়েছে। তিনি কতগুলি ঘুড়ি এনেছিলেন হিসাব করে দেখি।
সমাধানঃ
প্রতি ঝুড়িতে ঝুড়ির সংখ্যার সমান কমলালেবু রাখলে কমলালেবুর সংখ্যা হয় (1080+9) টি =1089 টি
∴ \(\sqrt{1089}=33\)
∴ তিনি 33 ঘুড়ি এনেছিলেন।
14. বকুলতলার একটি পুকুর সংস্কার করতে পঞ্চায়েত যতজন লোক নিযুক্ত করেছিলেন তারা ততদিন কাজ করে মোট 12375 টাকা পেয়েছেন। প্রত্যেকে দৈনিক যদি 55 টাকা পান, তবে কতজন লোক কাজ করেছিলেন হিসাব করে দেখি।
সমাধানঃ
মোট দিনসংখ্যা \(=\frac{12375}{55}=225\)
প্রত্যেককে দৈনিক 55 টাকা করে মোট 225 দিনের টাকা পেয়েছে।
∴ পুকুর সংস্কার করতে যতজন লোক নিযুক্ত হয়েছিল তাঁরা ততদিন কাজ করে।
\(225=15\times15={15}^2\)
∴ \(\sqrt{225}=15\)
∴ পুকুর সংস্কার করতে 15 জন লোক কাজ করেছিলেন।
15. চার অঙ্কের কোন বৃহত্তম পূর্ণবর্গ সংখ্যা 12, 18 ও 30 দ্বারা বিভাজ্য হিসাব করে দেখি।
সমাধানঃ
12, 18, 30 এর ল.সা.গু.
\(=3\times2\times2\times3\times5\)
= 180
∴ ক্ষুদ্রতম পূর্ণবর্গ সংখ্যা\(=180\times5=900\)
কিন্তু 900 চার অঙ্কের সংখ্যা নয়।
12, 18 ও 30 দ্বারা বিভাজ্য চার অঙ্কের পূর্ণবর্গ সংখ্যাগুলি হল
\(900\times4=3600\)
\(900\times9=8100\)
∴ চার অঙ্কের বৃহত্তম পূর্ণবর্গ সংখ্যাটি হল 8100 যা 12, 18, 30 দ্বারা বিভাজ্য।
16. পাঁচ অঙ্কের কোন ক্ষুদ্রতম পূর্ণবর্গ সংখ্যা 8, 15, 20 ও 25 দ্বারা বিভাজ্য হিসাব করে দেখি।
সমাধানঃ
8, 12, 20 ও 25 এর ল.সা.গু.
\(=5\times4\times2\times3\times5\)
= 600
যে ক্ষুদ্রতম পূর্ণবর্গ সংখ্যা 8, 12, 20 ও 25 দ্বারা বিভাজ্য সেটি হল
\(=600\times2\times3=3600\)
∴ যে পাঁচ অঙ্কের পূর্ণবর্গ সংখ্যা 8, 12, 20 ও 25 দ্বারা বিভাজ্য
সেগুলি হল \(3600\times4=14400,\)
\(3600\times9=32400,\)
\(3600\times16=57600,\) …
∴ পাঁচ অঙ্কের ক্ষুদ্রত্তম পূর্ণবর্গ সংখ্যাটি হল 14400 যা 12, 18, 30 দ্বারা বিভাজ্য।
0 Comments